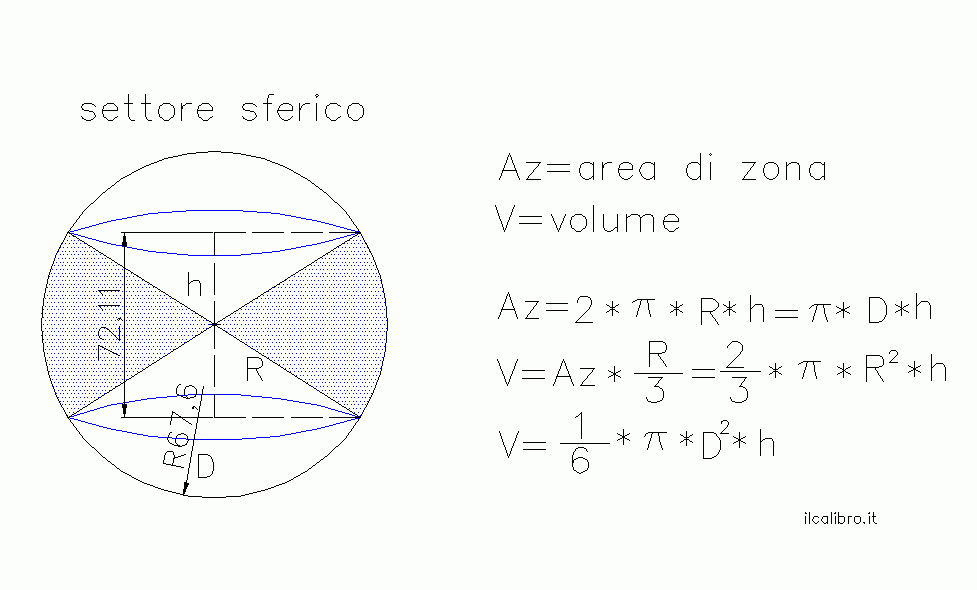Settore sferico

In geometria, un settore sferico è la porzione di una palla (comunemente detta "sfera") delimitata dalla superficie laterale di un cono retto avente il vertice nel centro della palla e dalla superficie laterale di una calotta sferica, essendo entrambi i solidi individuati da uno stesso piano secante alla palla, e quindi avendo essi la base in comune.

Si osserva che nel caso limite in cui il piano secante è diametrale l'angolo al vertice del cono è pari a π radianti e il settore sferico consiste quindi in un emisfero. Nel caso opposto, se il piano è tangente alla sfera, allora il settore sferico degenera nel segmento che unisce il centro della palla al punto di tangenza.

Proprietà

Volume

Siano r il raggio della sfera e h l'altezza della calotta sferica, il volume del settore sferico può essere scritto come:

${\displaystyle V={\frac {2\pi r^{2}h}{3}}\,}$

o anche come:

${\displaystyle V={\frac {2\pi r^{3}}{3}}(1-\cos \varphi )\,,}$

dove φ è un angolo di ampiezza pari alla metà dell'apertura del cono, ossia è l'angolo che esiste tra l'altezza del cono e il raggio della sfera.

Il volume del settore sferico è legato all'area della calotta sferica, A_s, dalla relazione:

${\displaystyle V={\frac {rA_{s}}{3}}\,.}$

Area

Siano r il raggio della sfera, a, il raggio della base della calotta sferica e h l'altezza della stessa calotta, la superficie del settore sferico, A, può essere scritta come:

${\displaystyle A=\pi r(a 2h)}$

o anche, utilizzando il precedentemente definito angolo φ:

${\displaystyle A=2\pi r^{2}(1-\cos \varphi )}$

Derivazione

La prima formula sopra mostrata per il calcolo volume del settore sferico può essere derivata dalla somma del volume del cono e di quello della calotta sferica che condividono la base circolare di raggio a:

${\displaystyle V=V_{c} V_{s}={\frac {\pi }{3}}\cdot a^{2}\cdot (r-h) {\frac {\pi }{3}}\cdot h^{2}\cdot (3\cdot r-h)}$

e considerando che, per il teorema di Pitagora: ${\displaystyle a^{2}=2\cdot h\cdot r-h^{2}}$.

La seconda formula può invece essere derivata integrando l'elemento di volume ${\displaystyle dV=\rho ^{2}\sin \phi d\rho d\phi d\theta }$ in coordinate sferiche:

${\displaystyle V=\int _{0}^{2\pi }\int _{0}^{\varphi }\int _{0}^{r}\rho ^{2}\sin \phi \,d\rho d\phi d\theta =\int _{0}^{2\pi }d\theta \int _{0}^{\varphi }\sin \phi d\phi \int _{0}^{r}\rho ^{2}d\rho ={\frac {2\pi r^{3}}{3}}(1-\cos \varphi )\,}$

Allo stesso modo, l'area può essere calcolata integrando l'elemento area sferica ${\displaystyle dA=r^{2}\sin \phi d\phi d\theta }$ in coordinate sferiche e ricordando che r è costante:

${\displaystyle A=\int _{0}^{2\pi }\int _{0}^{\varphi }r^{2}\sin \phi d\phi d\theta =r^{2}\int _{0}^{2\pi }d\theta \int _{0}^{\varphi }\sin \phi d\phi =2\pi r^{2}(1-\cos \varphi )\,,}$

dove φ è l'inclinazione e θ è l'azimut.

Note

Voci correlate

• Calotta sferica
• Spicchio sferico

Altri progetti

• Wikimedia Commons contiene immagini o altri file su Settore sferico

Collegamenti esterni

• (EN) Eric W. Weisstein, Spherical Sector, su MathWorld, Wolfram Research.